Digitalisierung

Kurven zu Zahlen

Digitale Aufzeichnungen sind längst zu unserem Alltag geworden, dennoch wissen die Wenigsten, was dahinter steckt und welche Qualitätskriterien die verschiedenen digitalen Systeme unterscheiden. An dieser Stelle werden einige wichtige Begriffe der Digitaltechnik erläutert.

Aus Analog wird Digital

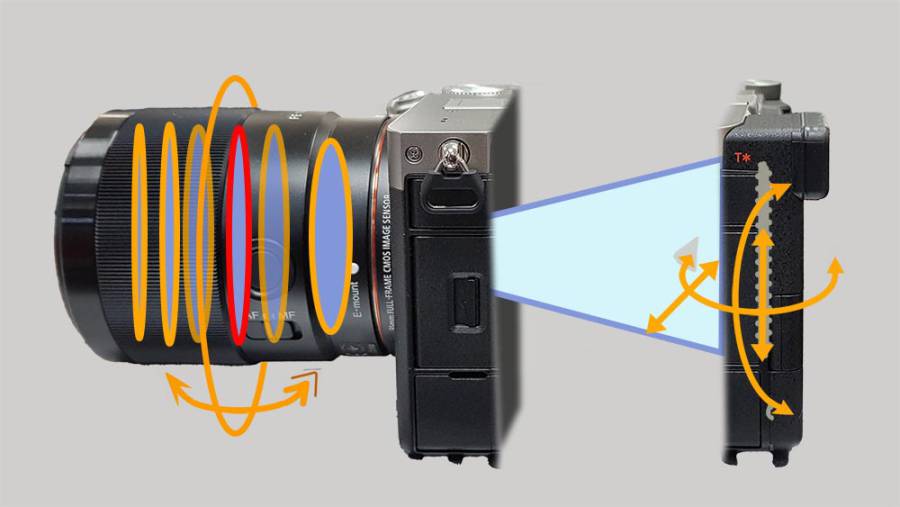
Die reale Welt, wie wir sie sehen und hören kennt kontinuierliche Wellen, um diese irgendwann verlustfrei speichern und bearbeiten zu können, müssen wir sie in ein digitales System umwandeln. Dafür werden die analogen Bild,- oder Tonsignale mit einer hohen Frequenz (mindestens doppelt so hoch wie die höchste Frequenz des analogen Signals) abgetastet.

Das bedeutet, wir messen den Pegelwert in regelmäßigen Abständen (bei Audio z.B. 44100, 48000 oder 96000 Mal in der Sekunde) nach. Die Signalgröße jeder einzelnen Messung wird in einen digitalen Wert umgewandelt. Dieser wird im sogenannten binären Zahlensystem ausgedrückt. 

Dieser Wert kann unterschiedlich differenziert sein, je feiner wir messen wollen, desto größer ist die sogenannte Wortbreite. Wenn wir Binärzahlen mit 8 Stellen zur Verfügung haben, sprechen wir von 8 Bit Wortbreite. Damit kann man 256 verschiedene Werte darstellen. DAT-Rekorder oder CDs arbeiten mit 16 Bit Wortbreite, sie können damit 65536 verschiedene Werte definieren. 

Definiert wird damit die Anzahl der Stellen der digitalen Zahlen, mit denen die entnommenen (gesampelten) Messwerte der analogen Signale ausgedrückt werden. Bis auf ganz wenige Ausnahmen, werden in der aktuellen Audio-Digitaltechnik Auflösungen verwendet, deren Anzahl der Stellen ein Vielfaches von 8 darstellt. Dies hängt mit Festlegungen im Zahlensystem heutiger Computer zusammen.

Werte ins Dualsystem umrechnen

Keine Sorge, Ihr Digitalgerät macht das automatisch, dennoch ist es nicht uninteressant zu wissen, auf welche Weise es geschieht: Wie werden ganzzahlige Werte in das Dualsystem umgewandelt? Anders als im Dezimalsystem, wo jede Stelle eine Verzehnfachung darstellt, wir also Einer, Zehner, Hunderter usw. kennen, bedeutet im Dualsystem jede Stelle nur eine Verdopplung der vorherigen Stelle.

Dazu müssen wir uns nur vor Augen führen, dass die Anzahl der darstellbaren Werte jeweils Potenzen der Zahl 2 darstellen. 8 Bit etwa ist nichts anderes als 2⁸, was wiederum 256 ergibt. 16 Bit ist 2¹⁶ und das ergibt 65536. Die Zahl Zwei spielt also eine wichtige Rolle bei dieser Berechnung:  

Die größte Zahl, die man mit 8 Bit abbilden kann ist rein rechnerisch die 255. Sie entsteht, indem man 128+64+32+16+8+4+2+1 zusammenrechnet. Da es auch den 0-Wert gibt, kommen wir insgesamt auf 256 mögliche Werte.

Man erstellt eine Liste, bei der man die Zahl, die man umrechnen will, jeweils durch 128 teilt und den Rest aus der Teilung Rechts vermerkt. Das Ergebnis der jeweils letzten Division schreibt man auf, den Rest dann in die nächste Zeile und teilt es  durch die nächstniedrigere Potenz von 2, also durch 64 und fährt fort bis man bei 1 angelangt ist.

Beispiel: Der Wert für 100 wird in 8 Bit als 01100100 dargestellt.

Werte, die größer sind als 256,  benötigen eine größere Wortbreite als 8 Bit. Die Messungen, die etwa bei einer Audio CD vorgenommen werden, haben die doppelte Wortbreite, also 16 Bit. Damit können auch Werte die größer sind als 256 abgebildet werden.

Datenmenge und Speicherbedarf

So seltsam es klingen mag, aber die Menge an Informationen, die durch die Digitalisierung analoger Signale entsteht, erfordert mehr Speicherplatz als das analoge Signal. Die Menge an Informationen vergrößert sich durch die Digitalisierung.

Wer digitale Audiosignale speichert oder gar per Mail-Anhang versenden möchte bekommt das recht eindrucksvoll zu spüren. So mancher E-Mail Account knickt bereits bei einem einzigen Musiktitel ein. Natürlich, es gibt die Möglichkeit der Datenkompression (etwa MP3), aber wer eine möglichst hohe Signalqualität aufzeichnen möchte, sollte davon Abstand nehmen.

Wie groß ist denn die Datenmenge, die bei Audiosignalen anfällt? Nun, es hängt, wie so oft in der digitalen Welt von der Qualität der Aufnahme ab. Je differenzierter und originalgetreuer wir unsere Aufnahmen machen wollen, desto größer wird die Datenmenge. Die Kriterien für die Qualität sind einerseits die Zahl der Messungen in der Sekunde, die sogenannte Sample-Rate (44.100, 48.000 oder 96.000 sind gängige Taktungen) sowie die Wortbreite (z.B. 8, 16, 24, 32 Bit).

Die obige Tabelle gibt Ihnen Aufschluss darüber, wie viel Festplattenbedarf Sie pro Minute Aufnahmezeit in den verschiedenen Auflösungen ohne Datenkompression in etwa verbrauchen.

Klirrfaktor digital

Nicht nur in der analogen Welt, auch in der digitalen tritt das Phänomen des Klirrfaktors auf. Wir meinen damit das Verhältnis von störenden Frequenzbestandteilen zum Ausgangssignal.

Bei der Umwandlung analoger Signale in digitale Werte führ die Quantisierung beim Abspielen zum Quantisierungsrauschen. Alle Werte, die zwischen den einzelnen Messungen (Samples) liegen, müssen auf- oder abgerundet werden. Bei diesen Rundungsvorgängen entsteht das Klirren (bzw. Rauschen). 

Je höher nun die Auflösung ist (also die Wortbreite, z.B. 8, 16, 32 Bit usw.) desto weniger muss gerundet werden und desto geringer die Rundungsfehler und damit das Klirren. Den Klirrfaktor im Verhältnis zu den Quantisierungsstufen kann man wie folgt berechnen:

Digitale Telefone arbeiten durchaus mit 4 Bit Wortbreite, da haben wir es mit nur 16 Quantisierungsstufen zu tun, was einem Klirrfaktur von 6,25 % entspricht. 

Bei 8 Bit Wortbreite, also 256 Quantisierungsstufen kommen wir auf einen Klirrfaktor von 0,39%, bei 16 Bit (die Auflösung der Audio-CD) und 65536 Stufen erzielen wir 0,0015 % Klirrfaktor. Das ist der Mindestwert, den man für Studioanwendungen fordern sollte.

Dithering

Studioaufnahmen werden, wenn sie digital erfolgen, mit einer möglichst hohen Qualität gemacht. Wortbreiten von 24, 32 oder 48 Bit sind durchaus üblich. Will man solche Aufnahmen auf ein Medium mit geringerer Wortbreite kopieren, so würden vor allem leise Passagen nicht mehr richtig aufgelöst werden und verzerren. 

Beim Herunterrechnen der Wortbreite treten zum Beispiel bei Ein- und Ausblenden von Signalen, dem Nachklingen von Instrumenten in den leisen Passagen Rundungsfehler auf. Diese Verzerrungen werden dann als sogenanntes Quantisierungsrauschen wahrgenommen.

Um diesen Problemen entgegenzuwirken werden diese Verzerrungen durch Hinzufügen eines „analogen“ Rauschens maskiert. Damit werden quasi die Lücken zwischen dem digitalen, regelmäßigen Quantisierungsrauschens (in der Frequenz der Sample-Rate) aufgefüllt und es wirkt natürlicher.

Die Aufnahme wird dabei geringfügig und nicht wieder rückgängig zu machen verändert, weshalb man den Vorgang des Ditherings in der Verarbeitungskette nur einmal am Ende anwenden sollte